Sr. Editor:
En los estudios longitudinales en cardiología, el objetivo principal suele ser el tiempo hasta ciertos eventos adversos (EA), con el objetivo de identificar factores de riesgo o la eficacia de un tratamiento. Tradicionalmente se han empleado los composite endpoints, en concreto los EA cardiovasculares mayores (MACE) en sus diferentes versiones, que presentan la gran ventaja de aumentar la potencia de los estudios y de simplificar el análisis, pero dificultan la interpretación de los resultados1 y además presentan otras limitaciones, como otorgar el mismo peso a cada evento o utilizar únicamente la información sobre el primer evento. Por ello, en los últimos años ha crecido la preocupación por la actualización de estos métodos2.
El problema de analizar datos de estudios longitudinales con varios EA de interés se presta de manera natural a ser abordado con modelos multiestado, ya que permiten plantear modelos con una estructura compleja de relaciones entre la aparición de los diferentes eventos teniendo en cuenta todos los datos disponibles para cada paciente, además de proporcionar información sobre el tiempo esperado y la probabilidad de aparición de cada EA, estableciendo su dependencia de los factores de riesgo o de las características del tratamiento3. Las principales ventajas de los modelos multiestado frente a otros modelos habitualmente utilizados se resumen en la tabla 1.
Table 1. Comparación de los modelos más habituales para datos de supervivencia en cardiología intervencionista y el modelo propuesto (multiestado)
| Composite endpoint (no longitudinal)a | Composite endpoint (longitudinal)b | Riesgos competitivosc | Multiestado | |
|---|---|---|---|---|
| Uso del primer evento | Sí | Sí | Sí | Sí |
| Uso del tiempo hasta el evento | No | Sí | Sí | Sí |
| Incluye todos los eventos | No | No | Sí | Sí |
| Puede incluir covariables (explicativas) | No | Sí | Sí | Sí |
| Distintos factores de riesgo para cada (tipo de) evento | No | No | Sí | Sí |
| Basado en la historia secuencial de eventos | No | No | No | Sí |
| Asume riesgos proporcionales | No | Sí | Sí | No |
| Modelo no paramétrico | Sí | No | No | Sí |
a Comparación de la proporción de MACE entre los grupos. b Estudio del riesgo de MACE, usualmente con el modelo de riesgos proporcionales de Cox. c Análisis del riesgo de un evento en presencia de otros eventos, usualmente con Fine & Grey. | ||||
Proponemos un modelo multiestado como alternativa al MACE para estudios longitudinales de cardiología intervencionista. Para demostrar su utilidad, se analizan los datos del estudio SYNERGY ACS4, con 1.008 pacientes con síndrome coronario agudo que recibieron una intervención coronaria percutánea entre 2013 y 2019. El estudio fue aprobado por un comité ético de referencia. Al tratarse de un estudio retrospectivo con anonimización de los datos, se eximió de la obtención del consentimiento informado. Como alternativa al MACE, planteamos un modelo multiestado, denominado disability model, en el que los pacientes entran (estado 1) en el momento del tratamiento, pasan al estado 2 cuando sufren un infarto o una nueva revascularización, o pasan al estado 3 al morir (figura 1). Este modelo permite considerar diferentes factores para cada una de las transiciones entre estados, además de evaluar el riesgo de muerte antes y después de los EA postratamiento. Se consideró un modelo de supervivencia no paramétrico para cada transición entre estados en los que se empleó el criterio de información de Akaike y la valoración clínica para la selección de covariables. El modelo fue ajustado con el paquete msm de R5.
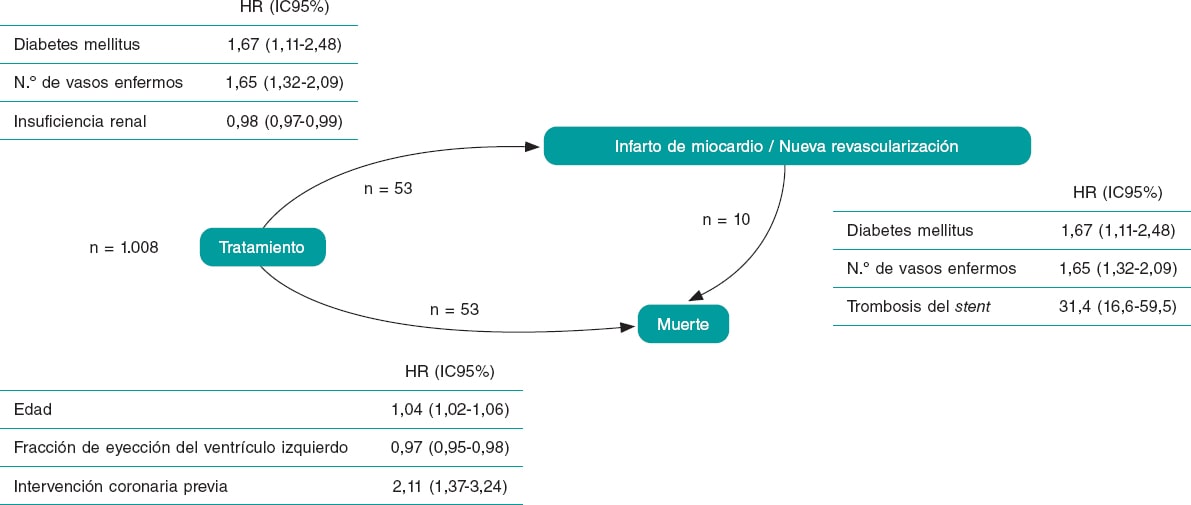
Figura 1. Estructura de estados del modelo propuesto. Los números junto a las transiciones representan el número de pacientes que presentaron el evento adverso correspondiente, partiendo de 1.008 pacientes. Las tablas muestran las covariables seleccionadas para el modelo de supervivencia de cada transición entre estados junto con sus correspondientes valores de hazard ratio (HR) y el intervalo de confianza del 95% (IC95%) asociado.
El seguimiento mediano fue de 856,52 días (Q1 = 546, Q3 = 1.115). La muerte es el EA más frecuente (6,25%), seguida de la revascularización (4,76%) y el infarto (3,08%). El modelo ajustado muestra que los factores asociados a infarto o revascularización son la diabetes, la insuficiencia renal y el número de vasos enfermos, mientras que la edad, la fracción de eyección del ventrículo izquierdo y la intervención coronaria percutánea previa se relacionan con la muerte (figura 1). Para ilustrar la utilidad del modelo definimos dos tipos de pacientes, de riesgo bajo y de riesgo alto, y representamos las probabilidades de pasar de un estado a otro durante el primer año después del tratamiento (figura 2).
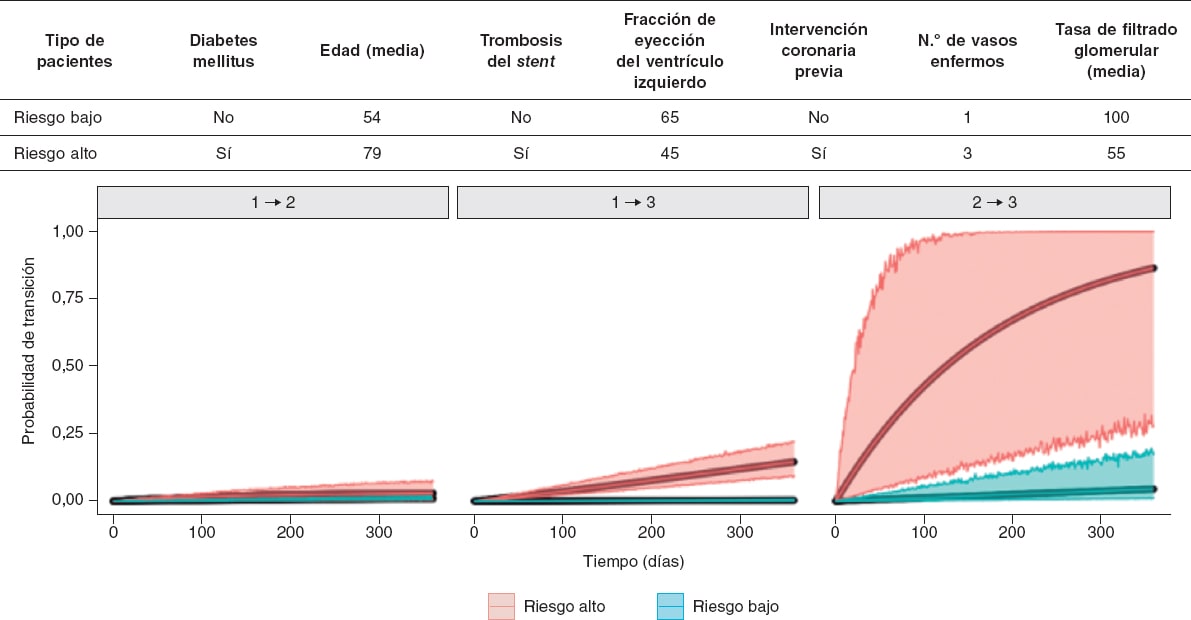
Figura 2. La tabla muestra las características de los pacientes definidos como de riesgo bajo y alto. Las figuras muestran la probabilidad del evento adverso correspondiente para cada transición durante el primer año después de la intervención coronaria percutánea para los pacientes de riesgo bajo (verde) y alto (rojo). La franja sombreada representa la incertidumbre de la estimación. En esta gráfica se aprecia que el pronóstico de los pacientes de riesgo alto es peor que el de los pacientes de riesgo bajo, así como la incertidumbre asociada al menor número de datos en la transición del estado 2 al 3 (de infarto/revascularización a muerte). Este tipo de pronóstico se podría hacer para las características concretas de un paciente dado.
Los resultados muestran el gran potencial de los modelos multiestado para el análisis de estudios longitudinales en cardiología intervencionista. Este método permite emplear la información sobre todos los EA de todos los pacientes, además de separar la contribución de los factores de riesgo para cada tipo de EA. A su vez, permite la modelización de la supervivencia después de haber sufrido un EA postratamiento. El modelo proporciona una predicción en términos de probabilidad y de tiempo esperado hasta cada tipo de EA para cada paciente (junto con la incertidumbre asociada) basada en sus características, el tratamiento y la evolución de su enfermedad, ofreciendo estimaciones personalizadas.
Por último, el modelo multiestado propuesto se ha utilizado con éxito en otras áreas de la medicina, aunque no está exento de limitaciones. En primer lugar, es necesario comprobar que se cumple la «propiedad de Markov», es decir, que la probabilidad de pasar del estado 2 al 3 no depende del tiempo empleado en llegar al estado 2, para poder asumirla. En caso de no cumplirse, la implementación del modelo resulta más complicada. En segundo lugar, aunque existe software disponible para implementar el modelo, no es sencillo de usar. En tercer lugar, el modelo hereda todas las limitaciones propias de los modelos no paramétricos. Las futuras versiones de este trabajo incluirán la inferencia bayesiana con modelos paramétricos y estructuras de estados más sofisticadas6.
FINANCIACIÓN
El presente trabajo ha sido financiado por la Universidad de León (có- digo 2020/00153/001, 2020) y por el MINECO (PID2019-104790GB-I00, 2020).
CONTRIBUCIÓN DE LOS AUTORES
Todos los autores contribuyeron al diseño del modelo multiestado. J.M. de la Torre-Hernández proporcionó los datos. N. Montoya y A. Quirós realizaron el análisis de los datos y la implementación del modelo. N. Montoya, A. Quirós y A. Pérez de Prado redactaron el manuscrito, y todos los autores contribuyeron sustancialmente al proceso de revisión.
CONFLICTO DE INTERESES
J.M. de la Torre-Hernández es editor jefe y A. Pérez de Prado es editor asociado de REC: Interventional Cardiology; se ha seguido el procedimiento editorial establecido en la revista para garantizar la gestión imparcial del manuscrito.
BIBLIOGRAFÍA
1. Hajihosseini M, Kazemi T, Faradmal J. Multistate models for survival analysis of cardiovascular disease process. Rev Esp Cardiol. 2016;69:710-716.
2. Hara H, van Klaveren D, Kogame N, et al. Statistical methods for composite endpoints. EuroIntervention. 2021;16:1484-1495.
3. Meira-Machado L, de Uña-Álvarez J, Cadarso-Suárez C, Andersen P. Multistate models for the analysis of time-to-event data. Stat Methods Med Res. 2009;18:195-222.
4. De la Torre Hernandez J, Moreno R, Gonzalo N, et al. The Pt-Cr everolimus stent with bioabsorbable polymer in the treatment of patients with acute coronary syndromes. Results from the SYNERGY ACS registry. Cardiovasc Revasc Med. 2018;20:705-710.
5. Jackson CH. Multi-State Models for Panel Data:The msm Package for R. J Stat Softw. 2011;38:1-29.
6. Armero C, Cabras S, Castellanos ME, et al. Bayesian analysis of a disability model for lung cancer survival. Stat Methods Med Res. 2016;25:336-351.
* Autor para correspondencia:
Correo electrónico: alicia.quiros@unileon.es (A. Quirós).