To the Editor,
The main objective of longitudinal studies conducted in cardiology is often time-to-adverse events (AE) to identify possible risk factors or the efficacy of treatment. Traditionally, composite endpoints have been used, often major adverse cardiovascular events (MACE) in their different versions. Their great advantage is to increase the statistical power of the studies and simplify analysis. However, they complicate the interpretation of results1 and have other limitations like giving the same weight to every event or using the information of the index event only. Therefore, over the last few years, concern has been growing on whether these methods should be updated.2
The problem with data analysis in longitudinal studies with several AE of interest can be approached using multi-state models in a natural way since they create models with a complex structure of relations during the appearance of different events and account for all the data available from every patient. Also, they provide information on time expected and probability of appearance of each AE, and establish their interdependence with risk factors or with the characteristics of treatment.3 The main advantages of multi-state models compared to other models commonly used are shown on table 1.
Table 1. Comparison between the most commonly used models regarding survival data in interventional cardiology and the multi-state model proposed
| Composite endpoint (non-longitudinal)a | Composite endpoint (longitudinal)b | Competitive risksc | Multi-state | |
|---|---|---|---|---|
| Use of index event | Yes | Yes | Yes | Yes |
| Use of time-to event | No | Yes | Yes | Yes |
| Includes all the events | No | No | Yes | Yes |
| It can include covariates (explanatory) | No | Yes | Yes | Yes |
| Different risk factors for every (type of) event | No | No | Yes | Yes |
| Based on the sequential history of events | No | No | No | Yes |
| Assumes proportional risks | No | Yes | Yes | No |
| Nonparametric model | Yes | No | No | Yes |
|
a Comparison of the number of MACE between the groups. b Study of the risk of MACE, often using Cox proportional hazard model. c Risk analysis of an event in the presence of other events often the Fine & Grey model. |
||||
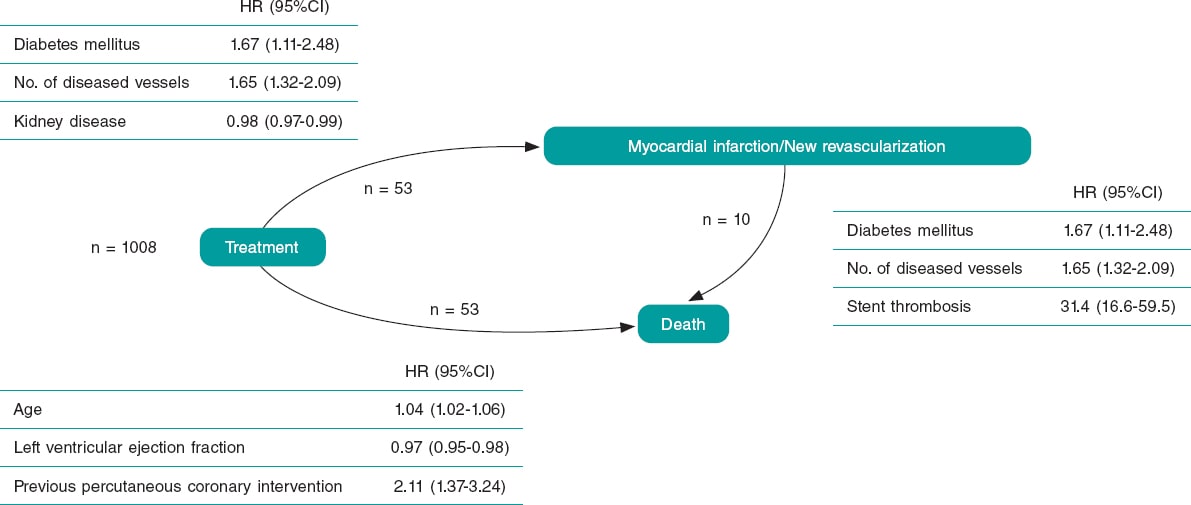
We propose a multi-state model as an alternative to MACE to conduct longitudinal studies in interventional cardiology. To demonstrate the utility of the model, data from the SYNERGY ACS trial4 of 1008 patients with acute coronary syndrome treated with percutaneous coronary intervention between 2013 and 2019 were analyzed. The study was approved by the local ethics committee. Since it was a retrospective study with data anonymization, no informed consent was required from the patients. As an alternative to MACE, we propose a multi-state model called disability model. In this model, patients are recruited while on treatment (state 1), when they have an infarction or receive a new revascularization (state 2) o when they die (state 3) (figure 1). In this model different factors for each transition among the 3 states can be included, as well as the risk of death before and after the occurrence of AE after treatment. A nonparametric survival model was considered for each transition among states using the Akaike information criterion, and clinical assessment for covariate selection. The model was adjusted using the MM spackage of R.5
Figure 1. Structure of the states of the model proposed. The numbers shown by the transitions represent the number of patients who suffered the corresponding adverse event starting at 1008 patients. Tables show the covariates selected for the survival model of each transition among the 3 states with their corresponding hazard ratios (HR), and the associated 95% confidence interval (95%CI).
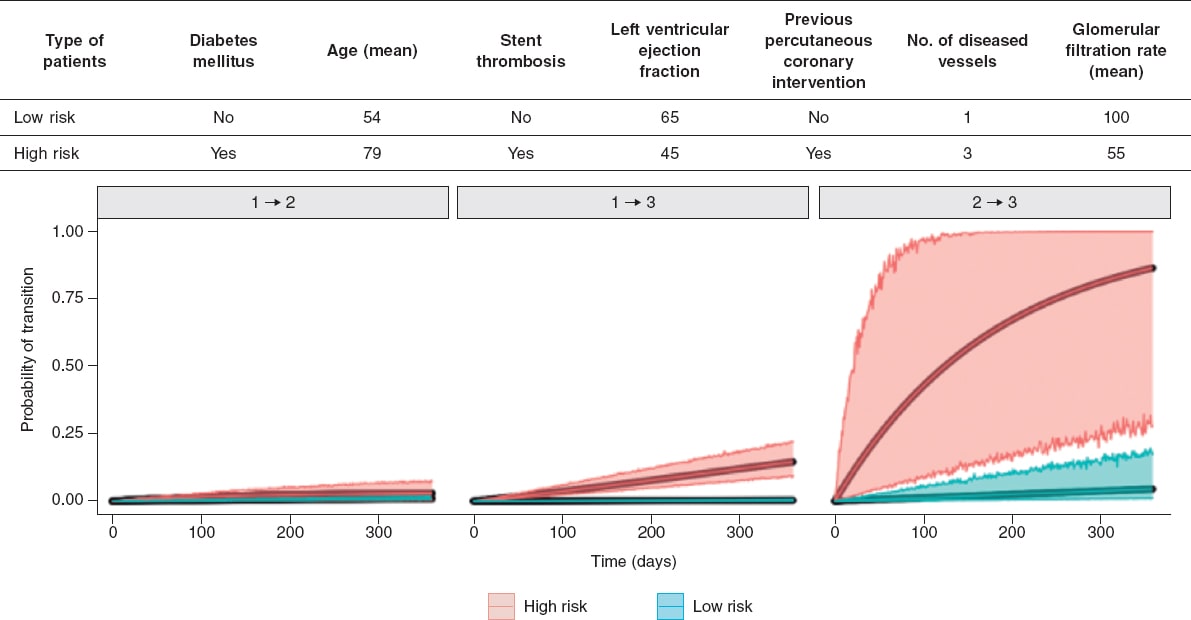
The median follow-up was 856.52 days (Q1 = 546, Q3 = 1115). The most common AE is death (6.25%), revascularization (4.76%) followed by infarction (3.08%). The adjusted model shows that the factors associated with infarction or revascularization are diabetes, kidney disease, and the number of diseased vessels. On the other hand, age, the left ventricular ejection fraction, and previous percutaneous coronary intervention are associated with death (figure 1). To illustrate the utility of the model we defined 2 types of patients (high and low risk) including the chances of moving from one state to the next within the first year after treatment (figure 2).
Figure 2. The table shows patients’ characteristics (defined as high- and low-risk patients). Figures show the probability of occurrence of a single adverse event associated with each transition within the first year after percutaneous coronary intervention for low-risk (green) and high-risk (red) patients. The shadow region represents uncertainty in the estimate. In this graph we can see that the prognosis of high-risk patients is worse compared to low-risk patients, as well as the uncertainty associated with fewer data in the transition from state 2 to state 3 (from infarction/revascularization to death). This type of prognosis could be made for the specific characteristics of every patient.
Results show a great potential of multi-state models in the analysis of longitudinal studies in interventional cardiology. This method allows us to use information on all AE occurred in all the patients while separating the contribution of risk factors for each type of AE. Also, a model of survival can be drawn after the occurrence of a single AE after treatment. This model is predictive regarding the probability and time expected until the occurrence of an AE in every patient (including the associated uncertainty as well) based on his characteristics, treatment, and disease progression, and provides individual estimates.
Finally, the multi-state model proposed has been successfully used in other fields of medicine. However, it has some limitations. In the first place, we need to see if it satisfies the «Markov property», that is, that the probability of moving from state 2 to state 3 do not depend on the time elapsed until reaching state 2 to assume such probability. If this property is not satisfied, the implementation of the model becomes more complicated. Secondly, although there is software available to implement it, it is not easy to use. In the third place, the model has all the limitations of nonparametric models. Future versions of this model will include Bayesian inference with parametric models and more sophisticated state structures.6
FUNDING
This study was funding by Universidad de León (code 2020/00153/001, 2020), and MINECO (PID2019-104790GB-I00, 2020).
AUTHORS’ CONTRIBUTIONS
All the authors contributed to the design of the multi-state model. J. M. de la Torre-Hernández provided data. N. Montoya, and A. Quirós analyzed data and implemented the model. N. Montoya, A. Quirós, and A. Pérez de Prado drafted this manuscript, and all the authors contributed substantially to the manuscript process of revision.
CONFLICTS OF INTEREST
J. M. de la Torre-Hernández is editor-in-chief, and A. Pérez de Prado is associate editor of REC: Interventional Cardiology; the journal’s editorial procedure to ensure impartial handling of the manuscript has been followed.
REFERENCES
1. Hajihosseini M, Kazemi T, Faradmal J. Multistate models for survival analysis of cardiovascular disease process. Rev Esp Cardiol. 2016;69:710-716.
2. Hara H, van Klaveren D, Kogame N, et al. Statistical methods for composite endpoints. EuroIntervention. 2021;16:1484-1495.
3. Meira-Machado L, de Uña-Álvarez J, Cadarso-Suárez C, Andersen P. Multistate models for the analysis of time-to-event data. Stat Methods Med Res. 2009;18:195-222.
4. De la Torre Hernandez J, Moreno R, Gonzalo N, et al. The Pt-Cr everolimus stent with bioabsorbable polymer in the treatment of patients with acute coronary syndromes. Results from the SYNERGY ACS registry. Cardiovasc Revasc Med. 2018;20:705-710.
5. Jackson CH. Multi-State Models for Panel Data:The msm Package for R. J Stat Softw. 2011;38:1-29.
6. Armero C, Cabras S, Castellanos ME, et al. Bayesian analysis of a disability model for lung cancer survival. Stat Methods Med Res. 2016;25:336-351.