RESUMEN
La estadística bayesiana valora de forma probabilística cualquier fuente de incertidumbre asociada a un estudio estadístico y utiliza el teorema de Bayes para actualizar, de manera secuencial, la información generada en las diferentes fases del estudio. Las características de la inferencia bayesiana la hacen especialmente útil para el tratamiento de datos cardiológicos procedentes de estudios experimentales u observacionales que contienen diferentes fuentes de variabilidad y complejidad. En este trabajo se presentan los conceptos básicos de la estadística bayesiana relativos a la estimación de parámetros y cantidades derivadas, predicción de nuevos datos y contrastes de hipótesis; estos últimos en el contexto de la selección de modelos o teorías.
Palabras clave: Distribución a posteriori. Distribución previa. Distribución predictiva. Probabilidad bayesiana. Teorema de Bayes.
ABSTRACT
Bayesian statistics assesses probabilistically all sources of uncertainty involved in a statistical study and uses Bayes’ theorem to sequentially update the information generated in the different phases of the study. The characteristics of Bayesian inference make it particularly useful for the treatment of cardiological data from experimental or observational studies including different sources of variability, and complexity. This paper presents the basic concepts of Bayesian statistics associated with the estimation of parameters and derived quantities, new data prediction, and hypothesis testing. The latter in the context of model or theory selection.
Keywords: Posterior distribution. Prior distribution. Predictive distribution. Bayesian probability. Bayes’ theorem.
Introducción: matemáticas, probabilidad y estadística
Según el conocido científico Stephen Hawking, el objetivo de la ciencia es «nothing less than a complete description of the universe we live in»1. Las científicas y los científicos perseguimos dicho objetivo construyendo teorías y valorando sus predicciones. Es la esencia del método científico.
La estadística es una disciplina científica que diseña experimentos y aprende de los datos. Formaliza el proceso de aprendizaje a través de observaciones y sirve de guía para la utilización del conocimiento acumulado en la toma de decisiones. Conceptos como azar, incertidumbre y suerte son casi tan antiguos como la propia humanidad, y reducir la incertidumbre ha sido siempre un deseo común de la mayoría de las civilizaciones. La probabilidad es el lenguaje matemático que cuantifica la incertidumbre y elemento fundamental del aprendizaje estadístico, que representa en términos probabilísticos tanto las poblaciones objeto de estudio como las muestras aleatorias procedentes de dichas poblaciones.
No existe una única metodología estadística. Las más conocidas y utilizadas son, con mucha diferencia, la estadística frecuentista y la estadística bayesiana. Ambas tienen objetivos comunes y utilizan la probabilidad como lenguaje del aprendizaje estadístico, aunque su diferente concepción de la probabilidad es el elemento que marca la gran diferencia entre ellas. Con la concepción frecuentista solo es lícito asignar probabilidades a fenómenos aleatorios que pueden definirse a través de experimentos que pueden repetirse muchas veces y siempre en condiciones idénticas e independientes.
La concepción bayesiana de la probabilidad es más amplia porque permite asignar probabilidades a cualquier elemento con incertidumbre, independientemente de su naturaleza. La probabilidad bayesiana se aplica a cualquier suceso aleatorio, tanto el que puede repetirse en las condiciones exigidas por la probabilidad frecuentista como aquel que no las cumple (probabilidad de que Arnau, persona de 60 años que vive solo en casa, se recupere de un ataque al corazón). Las diferencias entre ambas metodologías aún se amplían más porque la probabilidad bayesiana asigna probabilidades a parámetros (como la prevalencia de personas entre 45 y 65 años que han sufrido un ataque al corazón), a hipótesis estadísticas (la eficacia de un nuevo tratamiento para enfermos diabéticos con insuficiencia cardiaca es mayor que la de un tratamiento convencional), a modelos probabilísticos o, incluso, a datos faltantes generados por pérdidas de seguimiento no aleatorias (ignorar en un estudio de supervivencia sobre un proceso terminal la información de los enfermos con pérdida de seguimiento introduciría información sesgada en el estudio).
El segundo elemento diferenciador entre ambas metodologías estadísticas es la utilización del teorema de Bayes. Para la bayesiana es una herramienta fundamental para actualizar de forma secuencial la información relevante de un estudio. De esa forma, después de una primera fase de análisis, el conocimiento generado servirá como inicio de un nuevo proceso de aprendizaje que incorpore nueva información sobre el problema.
Las concepciones probabilísticas frecuentista y bayesiana comparten el mismo sistema axiomático y las mismas propiedades probabilísticas. Este nicho común las hace compartir un lenguaje matemático común.
Es difícil explicar el mapa de conceptos básicos bayesianos y sus relaciones sin entrar en muchos tecnicismos, y mucho más a través de estudios reales del mundo de la investigación cardiovascular. Por este motivo, en este artículo trabajaremos con ejemplos muy sencillos, que entendemos como potentes en términos conceptuales, pero simples y desprovistos de complejidades técnicas.
Este trabajo consta de siete secciones. La primera, esta introducción, presenta el marco de conocimiento general en el que se inserta la estadística bayesiana con relación a las matemáticas, la probabilidad y la estadística. La segunda muestra unas breves pinceladas históricas de la metodología bayesiana. Dedicamos la siguiente sección al teorema de Bayes en su versión más inocente para sucesos aleatorios. Seguidamente se abordan los conceptos y el protocolo básico de la estadística bayesiana: distribución previa, función de verosimilitud, distribución a posteriori y distribución predictiva para predecir resultados experimentales. También se explican brevemente los problemas computacionales inherentes a la aplicación práctica de los métodos bayesianos y se muestra su potencialidad para generar inferencias sobre cantidades derivadas relevantes. Los contrastes de hipótesis, especialmente el valor de p, se abordan más adelante, así como la propuesta bayesiana para contrastar hipótesis. El trabajo concluye con un pequeño comentario sobre la utilización de distribuciones previas.
CON BAYES, PRICE Y LAPLACE EMPEZÓ TODO
Conocer un poco de la historia bayesiana es importante porque permite situarla en una escala temporal y social que ilumina y potencia su aprendizaje. Esbozamos unas pequeñas pinceladas de algunos acontecimientos relevantes de esta historia. McGrayne2 cuenta de forma sencilla y rigurosa la historia completa.
Las primeras noticias del teorema de Bayes proceden de la Gran Bretaña de mitad del siglo xviii, con el reverendo Thomas Bayes intentando demostrar la existencia de Dios a través de las matemáticas. Nunca se atrevió a publicar sus resultados. A su muerte, legó todos sus ahorros a su amigo Richard Price para que, si lo consideraba oportuno, los gastara publicando sus trabajos. Price los publicó, pero pasaron prácticamente desapercibidos.
Seguimos en el siglo xviii, ahora en Francia con Pierre-Simon Laplace, uno de los matemáticos más brillantes de la historia. Descubrió, independientemente de Bayes y de Price, el teorema de Bayes en el formato que conocemos actualmente y desarrolló la concepción bayesiana de la probabilidad. Tras su muerte, sus trabajos fueron casi olvidados e incluso vilipendiados porque ya no estaban en sintonía con la idea imperante de objetividad que en aquellos días impregnaba el mundo de la ciencia.
Volvemos a Gran Bretaña. Bletchley Park era una mansión del siglo xix en el norte de Londres que se convirtió durante la Segunda Guerra Mundial (1939-1945) en el centro de los trabajos de descifrado de los mensajes secretos del ejército alemán. Alan Turing y su equipo, en el que destacamos al estadístico bayesiano Jack Good, tuvieron un papel clave en la historia de la estadística bayesiana: el teorema de Bayes fue una gran ayuda para descifrar el código de las máquinas Enigma que los alemanes utilizaban para cifrar y descifrar mensajes. Finalizada la guerra, el gobierno británico clasificó como secreto de estado toda información relacionada con Turing, las matemáticas, la estadística y las descodificaciones. El teorema de Bayes siguió siendo una buena herramienta para pocos científicos y un anatema (o peor) para la mayoría de ellos. Como anécdota especialmente reveladora, McGrayne2 cuenta que cuando Good presentó ante los miembros de la Royal Statistical Society británica los detalles del método que Turing y su equipo habían utilizado en el descifrado de los códigos nazis, las primeras palabras del siguiente orador fueron: «Tras estas estupideces […]».
En la segunda mitad del siglo xx, el futuro de la estadística bayesiana pintaba muy negro: pocos apoyos en el mundo académico anglosajón, casi desconocida en el resto de la comunidad científica y muchas dificultades de tipo computacional para aplicar la estadística bayesiana en estudios reales con datos. Pero no sucedió aquello que parecía que debía ocurrir. Seguimos en plena Segunda Guerra Mundial, ahora en el Laboratorio Nacional de Los Álamos del Estado de Nuevo México, en Estados Unidos. Este centro fue creado secretamente durante la Segunda Guerra Mundial para investigar la construcción de armas nucleares bajo el paraguas del Proyecto Manhattan, liderado por los Estados Unidos y con participación de Gran Bretaña y Canadá. Este entorno es el origen de los métodos de simulación Montecarlo, descubiertos en 1946 por el matemático polaco Stanislaw Ulam mientras jugaba un solitario. También aquí, Metropolis et al.3 publican el primer algoritmo de simulación Montecarlo basado en cadenas de Markov (MCMC) en el marco de sus investigaciones sobre la bomba H.
Durante muchos años no hay conexiones directas entre la estadística bayesiana y los métodos MCMC, aunque existen trabajos (especialmente en reconocimiento de imágenes) que ligarán ambos elementos4. Propiciados por los avances tecnológicos, en particular en materia computacional, Alan Gelfand y Adrian Smith, un norteamericano y un inglés, recogen los trabajos previos en métodos MCMC y los vinculan directamente con la estadística bayesiana5. Es el principio de la gran revolución bayesiana: comienza en el terreno de las aplicaciones para, poco a poco, impregnar también el mundo académico. La inferencia bayesiana es ahora reconocida, aceptada y valorada por la comunidad científica como una metodología estadística útil para el desarrollo científico y social.
TEOREMA DE BAYES
El formato más conocido del teorema de Bayes se presenta para sucesos aleatorios. Si A y B son sucesos aleatorios, entonces
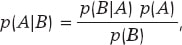
siendo p(A) la probabilidad del suceso A, p(A|B) la probabilidad asociada A pero condicionada por la información de que B ha ocurrido, y análogamente p(B)> 0 y p(B|A). Es importante distinguir entre las probabilidades p(A) y p(A|B). Ambas cuantifican la ocurrencia de A, pero p(A) lo hace de forma absoluta y p(B|A) de forma relativa y condicionada por la información recogida en B. Por ejemplo, nadie dudaría en pensar que la probabilidad de que una persona sufra una angina de pecho es mayor si se sabe que esa persona es hipertensa que si no se tiene esa información: p (Angina pecho | Hipertensión) > p (Angina pecho).
Ejemplo I: infecciones y test
La prevalencia de una determinada infección en cierta población es de 0,004. Se dispone de un test para detectar su presencia con una sensibilidad del 94% y una especificidad del 97%. Queremos valorar la probabilidad de que una persona de dicha población esté realmente infectada si se sabe que se ha hecho el test con resultado positivo para la infección.
Denotamos con V y Vc el suceso que describe si una persona tiene o no la infección, respectivamente. Por tanto, p(V) = 0,004 y p(Vc) = 0,996. Representamos por (+) y (–) un resultado positivo y negativo de la prueba para la infección, respectivamente. En términos probabilísticos, si una persona está infectada tendrá un resultado positivo con probabilidad 0,94 y un resultado negativo con probabilidad 0,06 p(+|V) = 0,94 y p(–|V) = 0,06 (falso negativo). Si no está infectada, la prueba resultará negativa con una probabilidad 0,97 y positiva con una probabilidad 0,03 p(–|Vc) = 0,97 y p(+|Vc) = 0,03 (falso positivo).
Según el teorema de Bayes, la probabilidad de que una persona esté infectada cuando ha tenido un resultado positivo para el test es
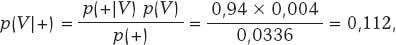
siendo p(+) = p(+|V) p(V) + p(+|Vc) p(Vc) = 0,0336 como consecuencia de la aplicación del teorema de la probabilidad total (figura 1).
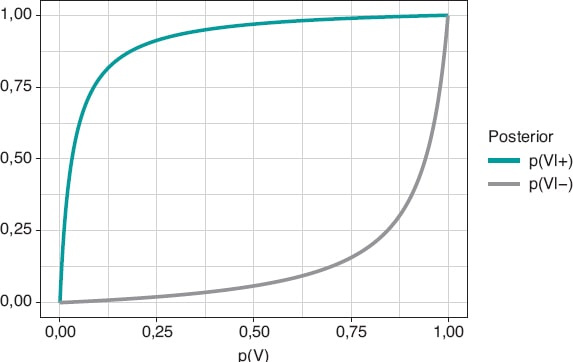
Figura 1. Probabilidad a posteriori de infección con un resultado positivo del test p(V|+) (gráfica superior) y con un resultado negativo p(V|–) (gráfica superior) en relación con la probabilidad a priori, p(V), de infección.
En principio, parece desconcertante que un test tan fiable y con un resultado positivo para la infección genere una probabilidad a posteriori pequeña, 0,112, a favor de la infección. Pero si nos fijamos en que la probabilidad inicial de tener la infección es p(V) = 0,004 y que después del resultado positivo del test es p(V|+) = 0,112, vemos que ha pasado de 4 a 112 por mil, se ha multiplicado por 28, y nos parece más relevante la influencia del resultado del test en dicha probabilidad a posteriori. En cualquier caso, necesitaríamos por lo menos una segunda prueba para aumentar la evidencia a favor o en contra de la infección.
La figura 2 muestra dos gráficas. La curva superior es la probabilidad a posteriori de la infección cuando el test ha dado positivo, p(V|+). La curva inferior corresponde también a la probabilidad de infección, pero con un resultado negativo del test, p(V|–). En ambos casos, dichas probabilidades a posteriori están representadas en términos de la probabilidad a priori, p(V), de tener la infección. Cuando p(V) está cerca de 0, como en este ejemplo, la probabilidad p(V|+) aumenta mucho, aunque en términos absolutos continúa siendo muy baja. Por el contrario, cuando p(V) está cerca de 1, la probabilidad p(V|–) continuará siendo alta a pesar de la evidencia en contra de un resultado negativo muy fiable. El elemento fundamental para entender esta situación es que la probabilidad a posteriori, p(V|+) = 0,112, combina una probabilidad muy pequeña de tener la infección con una probabilidad muy alta de un test positivo cuando se tiene la infección.
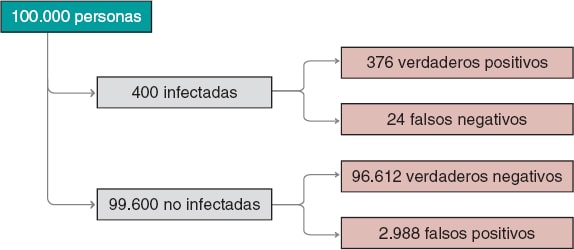
Figura 2. Número aproximado de personas infectadas, no infectadas, verdaderos positivos, verdaderos negativos, falsos positivos y falsos negativos en una población de 100.000 habitantes con una prevalencia inicial para la infección de 0,004 y un test con sensibilidad del 94% y especificidad del 97%.
Seguimos valorando los resultados obtenidos. La prevalencia de la infección, p(V) = 0,004, indica que en una población de 100.000 personas podríamos esperar alrededor de 400 infectadas y unas 99.600 no infectadas (figura 2). Si se realizara el test a toda la población esperaríamos que, aproximadamente, 376 de las 400 personas infectadas fueran positivas para el test (verdaderos positivos) y 24 no (falsos negativos). En el grupo de las personas sanas, el test resultaría negativo en alrededor de 96.612 personas (verdaderos negativos), pero positivo en aproximadamente 2.988 (falsos positivos). Si nos fijáramos en el número de personas con un test positivo, tendríamos 376 verdaderos positivos y 2.988 falsos positivos. Por tanto, la mayoría (en torno al 89%) de las personas con un test positivo no estarían realmente infectadas.
Una segunda repetición del test con un resultado también positivo aportaría mayor evidencia a favor de la infección. Su probabilidad debería actualizarse, incluyendo como nueva información el resultado positivo de la segunda prueba. Si representamos ahora por (+1) y (+2) un resultado positivo para la primera y la segunda pruebas, la probabilidad relevante sería p(V|+1,+2). La utilización secuencial del teorema de Bayes permite calcular dicha probabilidad considerando p(V|+1) = 0,112 como probabilidad a priori. El resultado obtenido, p(V|+1,+2) = 0,798, muestra una gran evidencia a favor de la infección después de dos resultados positivos de la prueba.
ESTIMACIÓN DE PARÁMETROS
Los estudios bayesianos básicos tienen como protagonistas a los modelos probabilísticos gobernados por parámetros desconocidos, que constituyen el foco de atención de la maquinaria inferencial bayesiana. Recordemos que un parámetro es una característica de una población estadística objeto de estudio. Ejemplos de parámetros son el porcentaje de efectividad de un fármaco, la tasa de supervivencia a 5 años del sarcoma de tejidos blandos, el factor básico de reproducción R0 de una infección, etc. Estimamos parámetros utilizando información parcial de la población objeto de estudio procedente de muestras de datos obtenidas mediante procedimientos aleatorios que garantizan su representatividad y su condición de miniatura de la población.
El modelo probabilístico más conocido es la distribución normal, con una función de densidad simétrica en forma de campana y definida a través de dos parámetros: la media (µ) y la desviación típica (σ). La media es el centro de gravedad de la distribución y corresponde al pico de la campana. La desviación típica es una medida de dispersión que determina la anchura de la campana: en todas las distribuciones normales, el intervalo (µ − 3σ, µ + 3σ) incluye el 99,7% de los valores de la distribución. Por lo tanto, la probabilidad asociada al intervalo (−3, 3) en una distribución normal con media 0 y desviación típica 1 será la misma que la asociada al intervalo (−6, +6) de una distribución normal con media 0 y desviación típica 2 (figura 3).
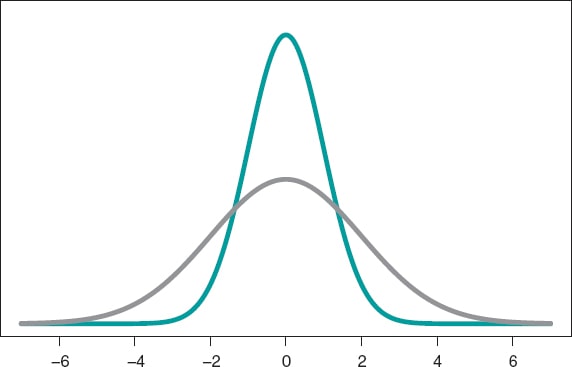
Figura 3. Gráfica de una densidad normal de media 0 y desviación típica 1 (color verde) y de una densidad normal de media 0 y desviación típica 2 (co-lor gris).
La media y la desviación típica son parámetros desconocidos en la mayoría de los estudios basados en datos normales. En nuestro caso, para evitar complicaciones técnicas, supondremos que la desviación típica es conocida y, por lo tanto, el proceso estadístico solo tendrá ojos para la media µ. El teorema de Bayes se adapta ahora al territorio de las distribuciones de probabilidad con la atención puesta en la media poblacional µ como parámetro de interés, según:
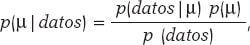
siendo p(μ) la distribución previa (o distribución a priori) de μ que cuantifica, en términos probabilísticos, la información inicial que se tiene sobre μ, y p(μ | datos) la distribución a posteriori de µ que contiene la información sobre µ que se tiene cuando a la información inicial se añade la de los datos. El término p(datos | μ) es la función de verosimilitud de μ, una medida que valora la compatibilidad de los datos con los posibles valores de μ. El elemento p(datos) es la distribución predictiva previa (también evidencia en contextos de aprendizaje automático [machine learning]) y valora la plausibilidad de los datos obtenidos.
Ejemplo II: corazón de niñas y niños con atrofia muscular
Falsaperla et al.6 presentan los resultados de un estudio observacional sobre el deterioro del sistema de conducción eléctrica del corazón que causa bradicardia o alteraciones en el electrocardiograma de niñas y niños con atrofia muscular espinal tipos 1 y 2 (AME1 y AME2, respectivamente). Nos hemos inspirado en este trabajo para construir un banco de datos simulado y, consecuentemente, los resultados de este ejemplo no proceden de Falsaperla et al.6 y no deberían compararse con los del trabajo original.
Simulamos datos de la longitud del intervalo PR, que se extiende desde el inicio de la despolarización auricular hasta el comienzo de la despolarización ventricular, de 14 niños con AME2. Asumimos un modelo normal con media desconocida y desviación típica conocida. Nuestro objetivo estadístico es estimar la media.
Seguimos el protocolo bayesiano. Necesitamos primero una distribución previa p(μ) que exprese nuestra información sobre dicho parámetro. Consideramos un escenario sin otra información sobre μ que no sea la de los datos y utilizamos la distribución de Jeffreys, que trata a todos los posibles valores de μ por igual7. La distribución a posteriori de μ, p(μ | datos), es una distribución normal con media 0,13 y desviación típica 0,03/√√14 segundos, que podemos ver representada gráficamente en la figura 4. Estimamos que μ es 0,13 segundos y valoramos directamente la precisión de dicha estimación a través de un intervalo de credibilidad que nos informa de que la probabilidad a posteriori de que μ tome valores entre 0,114 y 0,146 segundos es 0,95. Damos una probabilidad muy pequeña, 0,05, a que μ sea > 0,146 o < 0,114.
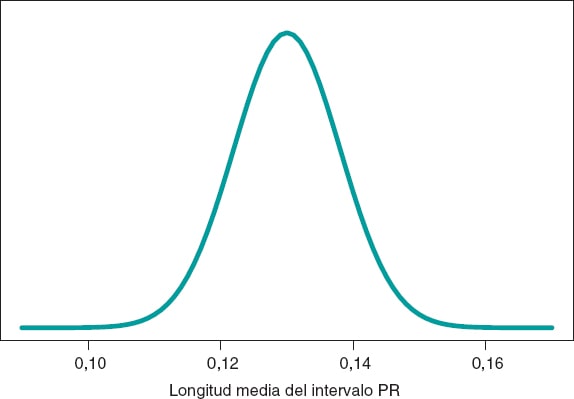
Figura 4. Distribución a posteriori de la longitud media del intervalo PR en niños afectados por atrofia muscular espinal tipo 2.
Un análisis frecuentista de estos datos nunca permitiría una eva luación probabilística directa sobre μ. Un intervalo de confianza frecuentista del 95% para μ proporcionaría los mismos resultados numéricos que el intervalo bayesiano, pero debería interpretarse de forma completamente diferente. La confianza frecuentista del 95% es sobre la capacidad del intervalo de incluir el verdadero valor de μ, y no sobre los posibles valores de μ. El intervalo construido, (0,114, 0,146), tiene una probabilidad de 0,95 de capturar el verdadero valor de μ, pero también una probabilidad de 0,05 de no hacerlo. Recordemos que la concepción frecuentista de la probabilidad impide asignar probabilidades a parámetros y no puede establecer valoraciones probabilísticas directas sobre μ.
PREDICCIÓN DE NUEVAS OBSERVACIONES
Predicción y estimación son conceptos estadísticos fundamentales. Estimamos parámetros, pero predecimos datos y resultados experimentales, siempre a través de distribuciones de probabilidad.
La distribución predictiva a posteriori para los resultados de un futuro experimento se construye combinando el modelo probabilístico, que relaciona los futuros datos y los parámetros, y la distribución a posteriori. Un aspecto importante del proceso predictivo respecto al de estimación es su mayor incertidumbre. De forma general, la precisión de las estimaciones mejora cuando aumenta el tamaño de la muestra, y en el caso hipotético de disponer de todos los datos, nuestra estimación sería exacta. Esta característica no la tiene el proceso de predicción. Aunque la precisión de las predicciones aumenta con el tamaño de la muestra, en el caso hipotético de acceder a toda la información poblacional nunca podrían establecerse predicciones sin error.
Ejemplo II: corazón de niñas y niños con atrofia muscular (continuación)
En la etapa de estimación, hemos estudiado la longitud media del intervalo PR en niñas y niños con AME2, aprendizaje basado en una muestra de 14 datos simulados. Contemplamos ahora una situación completamente diferente. Tenemos un niño con AME2 que no ha participado en el estudio y queremos predecir la longitud de su intervalo PR. El objetivo ahora no es estimar medias de la población con AME2, sino predecir el valor de la longitud del intervalo PR de un niño concreto.
La figura 5 muestra la distribución predictiva a posteriori de la longitud del intervalo PR de un nuevo niño con AME2. Esta predicción está basada en la información de los 14 niños de la muestra, pero hace referencia a un nuevo niño afectado por AME2. El valor predicho de la longitud del intervalo PR de este nuevo niño es 0,13 segundos. La precisión de la predicción se cuantifica a través de intervalos de predicción. En este caso, con probabilidad 0,95, el valor predicho se encontrará entre 0,069 y 0,191 segundos.
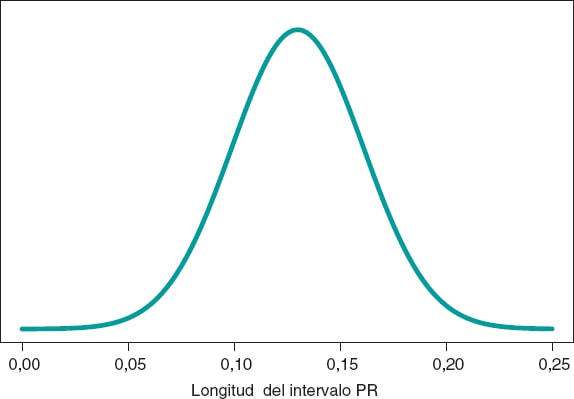
Figura 5. Distribución predictiva a posteriori de la longitud del intervalo PR de un nuevo niño con atrofia muscular espinal tipo 2.
SIMULACIÓN Y COMPARACIÓN DE GRUPOS
El protocolo bayesiano con los tres elementos básicos, distribución previa, función de verosimilitud y distribución a posteriori, es común a casi todo tipo de escenarios, básicos con pocos parámetros y complejos con muchas fuentes de incertidumbre con estructuras jerárquicas complicadas. Se trata de un protocolo sencillo y robusto que es conceptualmente potente y atractivo.
Las dificultades aparecen cuando queremos implementar este protocolo en estudios reales con cierta complejidad. En pocos casos puede obtenerse una expresión analítica para la distribución a posteriori de los parámetros, y resulta imposible para aquellas distribuciones a posteriori asociadas a cantidades de interés derivadas. En la mayoría de los estudios, las matemáticas se complican mucho y es imposible obtener las distribuciones a posteriori. En estos casos, los métodos MCMC son los salvadores del análisis bayesiano. Son capaces de simular muestras aproximadas de la distribución a posteriori relevante y generar, a partir de ellas, las inferencias o predicciones que el estudio requiera.
En el siguiente ejemplo ilustraremos la situación más básica que hemos comentado: a partir de una distribución (analítica) a posteriori diana simularemos distribuciones a posteriori de cantidades de interés relevantes no analíticas.
Ejemplo III: infarto agudo de miocardio y stents
Este ejemplo está inspirado en Iglesias et al.8. Se trata de un estudio con 1.300 pacientes con infarto agudo de miocardio sometidos a una intervención coronaria por vía percutánea. Cada paciente fue asignado aleatoriamente a un tratamiento con stents liberadores de sirolimus con polímero degradable (grupo S) o a un tratamiento con stents liberadores de everolimus con polímero durable (grupo E).
Comparamos ambos tratamientos en relación con la proporción de muertes a los 12 meses del tratamiento. De los 649 pacientes del grupo S, 35 renunciaron al tratamiento o se perdieron durante el primer año de seguimiento, y 24 murieron. En el grupo E, inicialmente con 651 pacientes, 25 se perdieron o renunciaron al tratamiento, y 22 murieron. La presencia de datos faltantes por pérdida de seguimiento es un tema importante que debe tratarse con cuidado. En este caso los obviaremos porque nuestro objetivo es ilustrar los procedimientos bayesianos con el menor tecnicismo posible.
Empezamos analizando el riesgo de muerte θs y θE en los grupos S y E, respectivamente, al cabo de 1 año de tratamiento. Como en ambos grupos cada persona puede morir o no durante el año de tratamiento, el modelo probabilístico en cada grupo es una distribución binomial que describirá el número de muertes registradas. El riesgo de muerte en cada grupo es una proporción, con valores entre 0 y 1. Seleccionamos como distribución previa para cada proporción una distribución β porque es un modelo probabilístico adecuado para proporciones y no presenta dificultades de cálculo. La distribución β (que representamos como Be(α, β)) tiene dos parámetros, α > 0 y β > 0, que determinan la forma de la distribución, así como su media y su varianza. Se trata de una distribución flexible, que puede ser simétrica o asimétrica, positiva o negativa (figura 6).
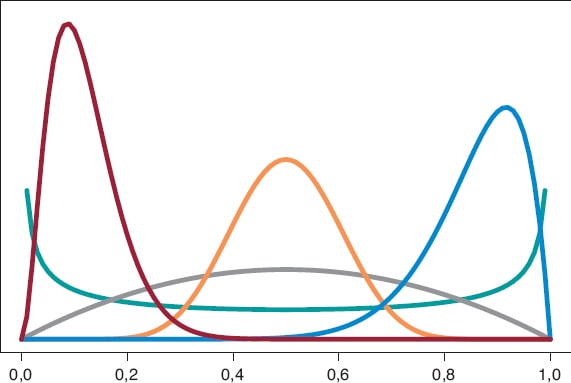
Figura 6. Gráfica de densidades β: Be(0,5, 0,5) en color verde, Be(2, 2) en color gris, Be(3, 22) en color granate, Be(12, 2) en color azul y Be(12, 12) en co-lor calabaza.
La distribución β a priori que mejor describe la ausencia de información es Be(0,5, 0,5). Su justificación solo obedece a criterios teóricos. La distribución a posteriori del riesgo de muerte en cada grupo será también una β cuyos parámetros actualizados se obtienen sumando el número de muertes y el número de personas vivas del estudio a los dos valores 0,5 y 0,5 de la distribución β a priori:
p(θs) = Be(0,5, 0,5); p(θs | datos) = Be(24,5, 590,5),
p(θE) = Be(0,5, 0,5); p(θE | datos) = Be(22,5, 604,5).
La estimación del riesgo de muerte en pacientes del grupo S y del grupo E es la media de su distribución a posteriori: 0,040 y 0,036, respectivamente. Además, con una probabilidad 0,95 el riesgo de muerte en el grupo S se encuentra entre 0,026 y 0,057, y en el grupo E entre 0,023 y 0,052. Estos resultados indican que la proporción de muertes en ambos grupos es pequeña, aunque ligeramente superior en el grupo S. El intervalo de credibilidad del 95%, tanto de θs como de θE, es muy informativo (figura 7).
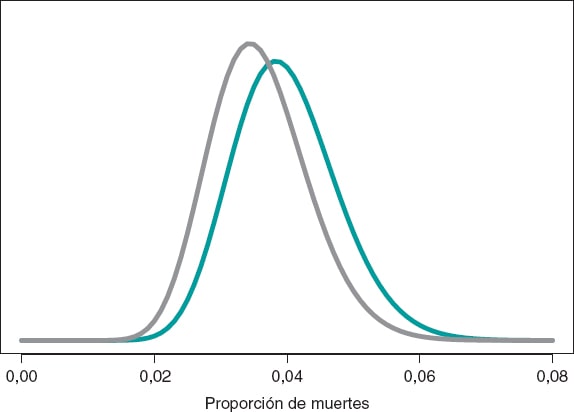
Figura 7. Distribución a posteriori de la proporción de muertes en pacientes del grupo S (color verde) y del grupo E (color gris).
Asumimos como objetivo la comparación del riesgo de muerte a 1 año en ambos grupos. Aunque la herramienta en la que primero podríamos pensar es los contrates de hipótesis (que introduciremos más adelante), la literatura epidemiológica y estadística sobre el tema es abundante y es habitual comparar dos grupos a través del riesgo relativo (RR) o del riesgo absoluto (RA)9. El RR de muerte al cabo de 1 año en pacientes con stents de tipo S frente a pacientes con stents de tipo E es RR = θs/θE, un cociente entre dos proporciones. Valores de RR < 1 indican que la proporción de muertes en el grupo S es menor que en el grupo E, y valores > 1 evidencian lo contrario. Puesto que el RR se define a través de θs y θE, la información de ambas proporciones, expresada mediante su distribución a posteriori, puede propagarse a RR como una distribución de probabilidad a posteriori, p(RR | datos) (figura 8). Esta distribución no es analítica, pero puede aproximarse a través de una simulación Montecarlo a partir de las dos distribuciones a posteriori, p(θs | datos) y p(θE | datos). De forma aproximada, la media a posteriori de RR es 1,160, su desviación típica es 0,346 y la probabilidad a posteriori de que RR sea > 1 es 0,641. Un análisis frecuentista análogo sería más complicado matemáticamente y no proporcionaría una valoración probabilística directa de RR.
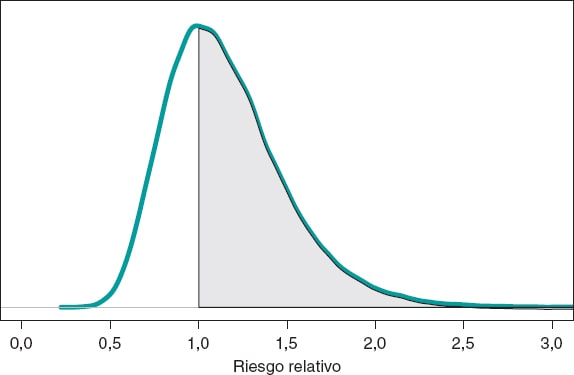
Figura 8. Distribución a posteriori del riesgo relativo de muerte al cabo de 1 año en pacientes con stents de tipo S frente a pacientes con stents de tipo E. El área de la región sombreada es la probabilidad, 0,641, de que la proporción de muertes en el grupo S sea mayor que en el grupo E.
Si comparamos ambos grupos según el RA de muerte al cabo de 1 año, nuestro objetivo sería RA = θs−θE. Se trata de una diferencia entre dos proporciones que podrá tomar valores entre −1 y 1. Valores negativos indicarán que la proporción de muertes en el grupo E es mayor que la del grupo S, y valores positivos indicarán lo contrario. La figura 9 muestra la distribución a posteriori de RA.
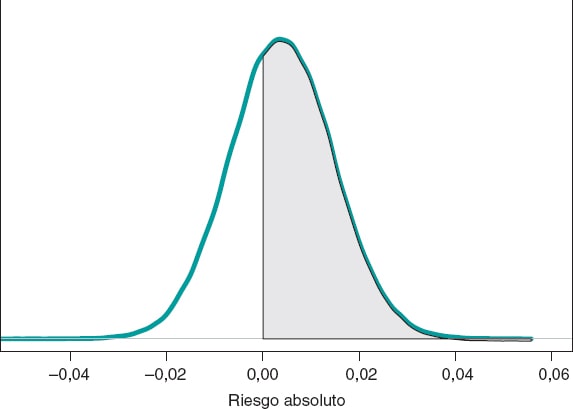
Figura 9. Distribución a posteriori del riesgo absoluto de muerte al cabo de 1 año en pacientes con stents de tipo S frente a pacientes con stents de tipo E. El área de la región sombreada es la probabilidad, 0,641, de que la proporción de muertes en el grupo S sea mayor que en el grupo E.
La media a posteriori de RA es 0,004, la desviación típica es 0,011 y con una probabilidad de 0,641 RA será > 0.
CONTRASTAR HIPÓTESIS: VALORES de p FRECUENTISTAS
Los contrastes de hipótesis son el tema que más discrepancias genera entre la comunidad científica bayesiana y frecuentista, porque es donde se evidencian más claramente las consecuencias de su diferente concepción de la probabilidad. Contrastar hipótesis es contrastar teorías. La mayoría de las nuevas teorías aparecen en el escenario científico de forma poco ruidosa y van acumulando, poco a poco, evidencia a su favor hasta que consiguen desbancar a las vigentes hasta ese momento.
El concepto más utilizado y conocido en la estadística frecuentista es el valor de p, así como su cifra de 0,05, que aparece en algunos estudios como un número mágico con el que se rechazan o aceptan hipótesis o teorías científicas. El valor de p es una herramienta propia de la inferencia frecuentista inexistente en la bayesiana para contrastar dos hipótesis: la hipótesis nula H0 (que suele representar la teoría científica vigente) y la hipótesis alternativa H1 (una nueva teoría). Los valores de p siempre están asociados a los datos, porque sin datos no hay valores de p. En estas condiciones, el significado del valor de p es la probabilidad de que un cierto resumen teórico de los datos sea igual al observado o más incompatible con la hipótesis nula en el supuesto de que dicha hipótesis sea cierta. Dicha compatibilidad viene marcada habitualmente por el umbral p = 0,05. Valores de p ≥ 0,05 mantienen la confianza en la hipótesis nula y valores de p < 0,05 favorecen la alternativa.
El uso excesivo, y a veces no adecuado, de los valores de p en estudios científicos es un tema de discusión en el mundo estadístico. Empezó en ambientes estadísticos reducidos y fue creciendo a medida que aumentaba el uso del valor de p más como un elemento «mágico» que como una herramienta científica. En 2014, la American Statistical Association, una de las sociedades estadísticas más importantes del mundo, abordó el tema y desarrolló un documento al respecto que se ha convertido en referente10. Algunas de las conclusiones sobre los valores de p relevantes para el tratamiento de datos biomédicos son:
1. Son una medida probabilística de la compatibilidad de los datos con la hipótesis nula. Cuanto más pequeño es un valor de p, más incompatibilidad muestran los datos con ella.
2. No valoran la probabilidad de que una hipótesis sea cierta ni tampoco de que no lo sea.
3. Las conclusiones de un estudio no deberían basarse únicamente en si un valor de p supera o no un determinado umbral. La utilización del término «estadísticamente significativo» (p < 0,05) para establecer conclusiones distorsiona cualquier procedimiento científico.
4. No proporcionan una medida del tamaño de un efecto ni de la importancia de un resultado. Cualquier efecto pequeño puede producir valores de p pequeños cuando el tamaño muestral o la precisión de las medidas es grande, y cualquier efecto grande puede producir valores de p grandes con muestras pequeñas u observaciones poco precisas.
Los valores de p han sido injustamente tratados porque se les han atribuido unas propiedades tan fantásticas e irreales que al final se han vuelto en su contra. Su discusión ha sacudido positivamente el debate científico y ha impulsado la crítica en disciplinas científicas que usan los datos para generar conocimiento. El enorme interés que despiertan en la actualidad los temas de reproducibilidad científica le debe mucho a ese debate11-15.
ACUMULAR EVIDENCIA PARA VALORAR PROBABILÍSTICAMENTE NUEVAS TEORÍAS
El concepto bayesiano de la probabilidad es el elemento clave para contrastar hipótesis y teorías, porque permite asignar probabilidades directas a hipótesis y teorías, tanto previas, p(teoría es cierta), como a posteriori, p(teoría es cierta|datos )16.
La estadística frecuentista basa su tratamiento de los contrastes de hipótesis en probabilidades del tipo p(datos|teoría es cierta), mientras que la estadística bayesiana lo basa en probabilidades de la forma p(teoría es cierta|datos). La probabilidad frecuentista p(datos|teoría es cierta) asume como cierta la teoría que se quiere contrastar y bajo esa suposición valora la concordancia de los datos con dicha hipótesis. La probabilidad bayesiana p(teoría es cierta|datos) valora probabilísticamente la certeza de la teoría objeto de análisis en relación con los datos obtenidos.
La herramienta fundamental de la estadística bayesiana para elegir entre las hipótesis
H0: la teoría 1 es cierta
H1: la teoría 2 es cierta
basándose en un conjunto de datos es el factor Bayes17, el cociente entre la probabilidad asociada a los datos según ambas teorías. Puede expresarse también como el cociente entre las odds a posteriori (p(la teoría 1 es cierta | datos ) / p(la teoría 2 es cierta | datos )) a favor de la certeza de la teoría 1 en relación a la de la teoría 2 y las correspondientes odds a priori (p(la teoría 1 es cierta) / p(la teoría 2 es cierta). De esta forma:
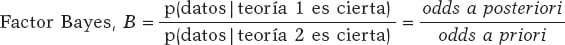
El factor Bayes (B) representa la evidencia a favor de la certeza de la teoría 1 (en relación a la de la teoría 2) proporcionada por los datos: transforma probabilidades a priori en probabilidades a posteriori. Al factor Bayes en escala logarítmica, log (B), se le conoce también como «peso de la evidencia», término que fue acuñado por Turing en Bletchley Park durante la Segunda Guerra Mundial. Valores pequeños del factor Bayes dan poco soporte a H0 frente a H1, y valores grandes proporcionan una fuerte cobertura a H0.
Ejemplo I: infecciones y test (continuación)
Retomemos los datos del ejemplo I: Vallivana necesita tener un diagnóstico sobre la infección con dos resultados positivos del test. Este problema puede plantearse como un contraste entre dos hipótesis:
H0: Vallibana tiene la infección
H1: Vallibana no tiene la infección
Asumimos que Vallibana no tiene ninguna característica especial que la haga tener una probabilidad de infección diferente que el resto de la población. Consecuentemente, sabemos que p(Vallibana tiene la infección) = 0,004 y p(Vallibana no tiene la infección) = 0,996. Las odds a priori para Vallibana a favor de la infección en relación con la no infección son:
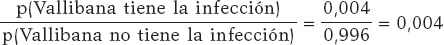
Vallibana se hace el test y sale positivo (+1). Decide repetírselo y vuelve a dar positivo (+2.). Las odds a posteriori para Vallibana a favor de la infección en relación con la no infección son:

El factor Bayes a favor de que Vallibana tenga la infección, o sea, el cociente entre las odds a posteriori y a priori, es 987,75. Este valor proporciona una fuerte evidencia a favor de que Vallibana esté realmente infectada (+).
Ejemplo II: corazón de niñas y niños con atrofia muscular espinal (continuación)
Volvemos al estudio de Falsaperla et al.6 del ejemplo II con el objetivo de comparar la longitud media del PR en niñas y niños con AME1 y AME2, que denotaremos μ1 y μ2, respectivamente, a través del contraste de hipótesis:
H0: μ2 ≤ μ1
H1: μ2 > μ1
en el que la hipótesis nula, H0, afirma que la longitud media del PR en niñas y niños con AME2 es menor o igual que en los niños con AME1. La hipótesis alternativa H1 afirma lo contrario. Continuamos trabajando con datos normales simulados en ambos grupos: n1 = 14 observaciones en el grupo AME1 con media y desviación típica muestral de 0,10 y 0,02 segundos, respectivamente, y n2 = 14 observaciones del grupo AME2 con media y desviación típica muestral de 0,13 y 0,03 segundos, respectivamente.
Construimos un proceso inferencial para la media de cada grupo por separado. En ambos casos, consideramos una distribución previa neutra que conceda todo el protagonismo a los datos. La figura 10 muestra la distribución a posteriori de la media de cada grupo. Ambas distribuciones están bastante separadas, por lo que las probabilidades a posteriori asociadas a cada hipótesis son bastante diferentes: 0,002 para H0 y 0,998 para H1.
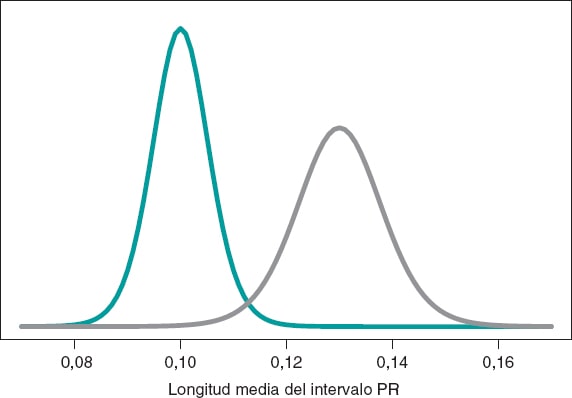
Figura 10. Distribución a posteriori de la longitud media del intervalo PR en niñas y niños afectados por atrofia muscular espinal tipo 1 (color verde) y tipo 2 (color gris).
p(H0|datos) = p(μ2 ≤ μ1|datos) = 0,002
p(H1|datos) = p(μ2 > μ1|datos) = 0,998
Aproximadamente es 500 veces más probable que H1 sea cierta que no lo sea. Ante tal cantidad de evidencia, la decisión más sensata es elegir H1. El tratamiento frecuentista de este contraste se basa en el valor de p. En nuestro caso, obtendríamos un valor de p = 0,002, que implicaría rechazar la hipótesis nula en favor de la alternativa. Ambas metodologías proponen la misma decisión y proporcionan los mismos resultados numéricos: probabilidades de 0,002; sin embargo, ambas probabilidades son conceptualmente distintas. La probabilidad bayesiana valora la hipótesis nula en relación con los datos observados, mientras que la probabilidad frecuentista valora los datos observados en el supuesto de que la hipótesis nula sea cierta.
Seguimos inspirándonos en Falsaperla et al.6 y recordamos que nuestros ejemplos no están basados en los trabajos originales y que solo tienen objetivos ilustrativos de los procedimientos bayesianos. Trabajamos ahora con la longitud de la onda P del electrocardiograma. Queremos comparar la longitud media de dicha onda en niños con AME1 y con AME2. Simulamos 14 observaciones de la longitud de la onda P en el grupo de niños con AME1 y en el de niños con AME2. La media y la desviación típica muestral son 0,09 y 0,05 segundos en el grupo AME1, respectivamente, y 0,07 y 0,03 segundos en el grupo AME2. Comparamos las medias de ambos grupos a través del contraste de hipótesis:
H0: media onda P en AME1 = media onda P en AME2
H1: media onda P en AME1 > media onda P en AME2
según un proceso inferencial bayesiano similar al del ejemplo anterior. La figura 11 muestra la distribución a posteriori de la longitud media de la onda P en ambos grupos. Puede observarse que los datos del grupo de niñas y niños con AME2 son menores que los del grupo con AME1. La probabilidad a posteriori asociada a cada hipótesis es:
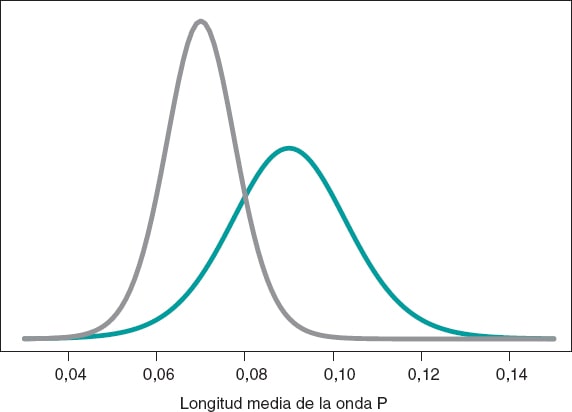
Figura 11. Distribución a posteriori de la longitud media de la onda P en niñas y niños afectados por atrofia muscular espinal tipo 1 (color verde) y tipo 2 (color gris).
p(H0 | datos) = p(media onda P en AME1 ≤ media onda P
en AME2 | datos)
p(H1 |datos) = p(media onda P en AME1 > media onda P
en AME2 | datos)
Estos resultados proporcionan una notable evidencia a favor de la hipótesis alternativa, que es casi 8 veces más probable que H0. Desde el punto de vista frecuentista, el valor de p asociado a los datos sería 0,107 (> 0,05), por lo que concluiríamos afirmando que los datos no proporcionan evidencia para rechazar H0. La decisión bayesiana podría ser perfectamente la misma, pero el análisis bayesiano proporciona la valoración directa de la certeza de ambas hipótesis. Los resultados del análisis bayesiano podrían aprovecharse como información previa en un futuro estudio con más datos. De esta forma, las distribuciones a posteriori obtenidas (figura 11) serían las distribuciones previas en ese nuevo estudio. El teorema de Bayes permite generar conocimiento de forma secuencial para buscar evidencia a favor o en contra de las hipótesis.
ALGUNAS DUDAS QUE PLANTEA LA CARDIOLOGÍA SOBRE LA APLICACIÓN DE LA METODOLOGÍA EN ESTUDIOS CLÍNICOS
Uno de los temas más controvertidos en la metodología bayesiana es la selección de distribuciones previas. Un análisis bayesiano permite siempre la posibilidad de no utilizar ninguna información sobre la cantidad de interés que no sea la proporcionada por los datos. En este caso, se trabaja con distribuciones previas que desempeñan un papel neutro en el proceso de aprendizaje, que únicamente sirven como punto de partida para el inicio del protocolo inferencial bayesiano.
Las distribuciones previas informativas contienen información adicional a la proporcionada por los datos, como por ejemplo conocimiento experto18-20 o resultados de estudios anteriores21,22. Se trata de una característica bayesiana muy valiosa en estudios en los que se dispone de pocos datos, como por ejemplo enfermedades raras y medicamentos huérfanos. Es importante co-mentar que los procesos inferenciales basados en previas informaciones deberían incluir un análisis de sensibilidad de los resultados obtenidos con respecto a la(s) distribución(ones) previa(s) utilizada(s). Asimismo, es cada vez más frecuente considerar comunidades de distribuciones previas, con distribuciones pre vias diversas, más o menos escépticas o entusiastas con el efecto que se desea probar, porque proporcionan un marco científico de referencia.
En los ensayos clínicos, la utilización de distribuciones previas informativas permite, en muchas ocasiones, reducir los tamaños muestrales frecuentistas basados en valores preasignados de la potencia del test y en estimaciones previas de los parámetros22. Un ejemplo de dicha situación es el estudio BIOSTEMI8. La muestra de 1.300 pacientes fue estimada por métodos bayesianos a través de una distribución previa robusta en forma de mixtura que incorpora en igual proporción información histórica de 407 pacientes procedentes del ensayo BIOSCIENCE23 y una distribución prácticamente no informativa. La flexibilidad del aprendizaje secuencial bayesiano es un elemento clave en los llamados diseños bayesianos adaptativos24, que permiten incorporar información adicional en diferentes fases del ensayo sin que peligren la consistencia y la fiabilidad de sus resultados.
FINANCIACIÓN
Este trabajo ha sido subvencionado parcialmente por Biotronik Spain S.A. y por el proyecto PID2019-106341GB-I00 del Ministerio de Ciencia e Innovación del Gobierno de España.
CONTRIBUCIÓN DE LOS AUTORES
C. Armero es la responsable de la estructura, el contenido y la escritura del trabajo. P. Rodríguez y J.M. de la Torre Hernández han participado en la revisión del trabajo de forma activa.
CONFLICTO DE INTERESES
C. Armero, P. Rodríguez y J.M. de la Torre Hernández declaran no tener ningún conflicto de intereses con respecto al contendido, la autoría y la publicación de este trabajo. J.M. de la Torre Hernández es editor jefe de REC: Interventional Cardiology. Se ha seguido el procedimiento editorial establecido en la revista para garantizar la gestión imparcial del manuscrito.
BIBLIOGRAFÍA
1. Hawking S. A Brief History of Time:The Origin and Fate of the Universe. New York:Bantam;1988.
2. McGrayne SB. La teoría que nunca murió:De cómo la regla de Bayes permitiódescifrar el código Enigma, perseguir los submarinos rusos y emerger triunfante de dos siglos de controversia. Barcelona:Crítica;2012.
3. Metropolis N, Rosenbluth A, Rosenbluth M, Teller A, Teller E. Equations of state calculations by fast computing machines. J Chem Phys. 1953;21:1087-1092.
4. Robert CP, Casella G. A Short History of Markov Chain Monte Carlo:Subjective Recollections from Incomplete Data. Stat Sci. 2011;26:102-115.
5. Gelfand AE, Smith AFM. Sampling-based approaches to calculating marginal densities. J Am Stat Assoc. 1990;85:398-409.
6. Falsaperla R, Vitaliti G, Collotta AD, et al. Electrocardiographic Evaluation in Patients With Spinal Muscular Atrophy:A Case-Control Study. J Child Neurol. 2018;33:487-492.
7. Robert CP, Chopin N, Rousseau J. Harold Jeffreys's Theory of Probability Revisited. Stat Sci. 2009;24:141-172.
8. Iglesias JF, Muller O, Heg D, et al. Biodegradable polymer sirolimus-eluting stents versus durable polymer everolimus-eluting stents in patients with ST-segment elevation myocardial infarction (BIOSTEMI):a single-blind, prospective, randomised superiority trial. Lancet. 2019;394:1243-1253.
9. Christensen R, Johnson W, Branscum A, Hanson TE. Bayesian Ideas and Data Analysis:An Introduction for Scientists and Statisticians. Boca Raton:CRC Press;2011.
10. Wasserstein RL, Lazar NA. The ASA Statement on p-Values:Context, Process, and Purpose. Am Stat. 2016;70:129-133.
11. Goodman SN. Toward Evidence-Based Medical Statistics. 1:The P Value Fallacy. Ann Intern Med. 1999;130:995-1004.
12. Greenland S, Senn SJ, Rothman KJ, et al. Statistical tests, P values, confidence intervals, and power:a guide to misinterpretations. Eur J Epidemiol. 2016;31:337-350.
13. Halsey LG, Curran-Everett D, Vowler SL, Drummond GB. The fickle P value generates irreproducible results. Nat Methods. 2015;12:179-185.
14. Ioannidis JPA. Why Most Published Research Findings Are False. PLoS Med. 2005;2:e124.
15. Ioannidis JPA. The Proposal to Lower P Value Thresholds to .005. J Am Med Assoc. 2018;319:1429-1430.
16. Kruschke JK. Doing Bayesian data analysis:A Tutorial with R, JAGS, and Stan. 2nd ed. Amsterdam:Academic Press/Elsevier;2015.
17. Kass RE, Raftery AE. Bayes Factors. J Am Stat Assoc. 1995;90:773-795.
18. Hampson LV, Whitehead J, Eleftheriou D, et al. Elicitation of Expert Prior Opinion:Application to the MYPAN Trial in Childhood Polyarteritis Nodosa. PLoS One. 2015;10:e0120981.
19. Mason AJ, Gomes M, Grieve R, Ulug P, Powell JT, Carpenter J. Development of a practical approach to expert elicitation for randomised controlled trials with missing health outcomes:Application to the IMPROVE trial. Clin Trials. 2017;14:357-367.
20. Jansen JO, Wang H, Holcomb JB, et al. Elicitation of prior probability distributions for a proposed Bayesian randomized clinical trial of whole blood for trauma resuscitation. Transfusion. 2020;60:498-506.
21. Grant RL. The uptake of Bayesian methods in biomedical meta-analyses:A scoping review (2005–2016). J Evidence-Based Med. 2019;12:69-75.
22. Spiegelhalter DJ, Abrams KR, Myles JP. Bayesian Approaches to Clinical Trials and Health-Care Evaluation. Chichester:Wiley;2004.
23. Pilgrim T, Heg D, Roffi M, et al. Ultrathin strut biodegradable polymer sirolimus-eluting stent versus durable polymer everolimus-eluting stent for percutaneous coronary revascularisation (BIOSCIENCE):a randomised, single-blind, non- inferiority trial. Lancet. 2014;384:2111-2122.
24. Schmidli H, Gsteiger S, Roychoudhury A, O'Hagan A, Spiegelhalter D, Neuenschwander B. Robust meta-analytic-predictive priors in clinical trials with historical control information. Biometrics. 2014;70:1023-1032.
* Autor para correspondencia:
Correo electrónico: Carmen.armero@uv.es (C. Armero).