Bayesian vs frequentist statistics: afraid of losing the reference?

While on his first hospital duty, a second-year cardiology resident receives a message in his pager about a patient who has just been admitted to the emergency room with chest pain. Specifically, he is asked to discard that the pain is of coronary origin. The resident questions the patient on his symptoms, examines his risk factors, and analyzes the electrocardiogram (ECG). With the ECG data, the qualitative information of pain provided by the patient, together with his past medical history, the presence of coronary pain is eventually discarded. The patient’s past medical history reads «the symptoms described by the patient, the presence of hypertension as the only risk factor, and the lack of specific changes on the ECG suggest that the chances of coronary pain are extremely low». Intuitively, the resident considers that the chances the pain is due to coronary artery disease (CAD) with the data available (qualitative data of pain, risk factors, ECG) is lower than, let’s say, 5%. In other words, the resident instinctively concludes that:

p(CAD |qualitative data, risk factors, ECG) < .05,

that is, the probability of having CAD according to all the abovementioned information (qualitative data, risk factors, and ECG) is < 5%.

However, before the patient is discharged, the resident decides to consult with the fifth-year cardiology resident who is at the Coronary Care Unit. He arrives to the emergency room and asks the patient about his symptoms, examines his medical history, and crosschecks his ECG once again. The much more experienced fifth-year resident considers that, although there are no risk factors other than hypertension, certain characteristics of the pain could have a coronary origin. And not only that, the analysis of the ECG reveals minimal repolarization alterations that appear as a mild—almost unnoticeable—rectification of the ST-segment. Intuitively, the resident considers that the chances that the pain is due to coronary artery disease (CAD) is undoubtedly > 5%, and possibly > 20%. In other words, the fifth-year resident intuitively concludes that:

p(CAD |qualitative data, risk factors, ECG) > .02

that is, the probability of having CAD according to all the information provided above (qualitative data, risk factors, and ECG) is > 20%.

With this early assessment, the fifth-year resident decides to perform a transthoracic echocardiogram (TTE) that reveals alterations in segmental contractility. With this new information available, the resident believes that the chances that the pain is of coronary origin have increased significantly:

p(CAD |qualitative data, risk factors, ECG, TTE) > .05

The intuition of a moderate-high probability of the coronary origin of the pain plus the information provided by the TTE suggest that high-sensitivity troponin (Tp) level should be tested, as Tp appears slightly elevated. Therefore, the intuitive probability that the patient’s chest pain is of coronary origin increases even more:

p(EC |qualitative data, risk factors, ECG, TTE, Tp) > .08

The previous example—though rather simplistic—illustrates several factors associated with conditioned probability and, more specifically, with traditional Bayes’ theorem.

Firstly, it illustrates how Bayes’ theorem is possibly a very appropriate mathematical approach to update our natural and intuitive decision making in medicine: we take an effect—which is what we find at the patient’s bedside—(chest pain), and make a decision on its cause with diagnostic, prognostic or treatment purposes, and then intuitively assign a probability to the cause under consideration (coronary artery disease). We do this with the information available we believe to be the effects of this cause while considering other variables closely associated with the cause such as the characteristics of pain, the ECG, the risk factors, etc.

Secondly, it illustrates how different sources of information added sequentially provide a more accurate definition on the probability of a given cause, always intuitively. And not only that, in the routine clinical practice, interpreting different sources of information varies from observer to observer, which will determine that the probability assigned to a given cause will vary significantly among observers. Here the clinician’s experience undoubtedly plays a key role.

This example also indirectly illustrates how difficult it is to obtain numerical—though approximate—estimates of the actual probability of the real cause for the effect (CAD) from the effects seen and other variables associated with this cause. As Armero et al.1 state in an article recently published in REC: Interventional Cardiology, the accurate probability estimate of the example would require solving the equation of Bayes’ theorem:

p(CAD |information available) =

where information available, in the example, would be the qualitative data of pain, the risk factors, the ECG, etc. But here is where problems begin. Like Armero et al.1 say, the first problem is to obtain the prior distribution to estimate probabilities. Although estimates can be made on the probability of CAD in a population based on its prevalence or on the probabilities of hypertensive patients or on the probabilities of having an abnormal ECG, estimating the probability of the qualitative data of pain doesn’t have a clear distribution on which to lean on. Like Armero et al.1 say the second problem is implementing an analytical expression for the posterior distribution of parameters and estimating the function of verisimilitude. Again, although the probability of knowing that a hypertensive patient has CAD or that an ECG shows certain characteristics of coronary artery disease is feasible, the problem becomes more complicated when several sources of information are combined; what are the chances of having chest pain with certain characteristics in a hypertensive patient with a given ECG knowing that he’s got CAD? Although it is true that distribution samples can be simulated, the analytical method becomes complicated and—as Armero et al.1 say—interpretation probably stops being intuitive.

We should also add the problem of «expert knowledge» to the mix for the definition of prior distribution. Like the example illustrates, knowledge can depend on the expert’s interpretation. But also, to a great extent, prior knowledge can significantly be affected by publication bias or it can be erroneous, which is why the associated informative distribution will give rise to biased probability estimates.

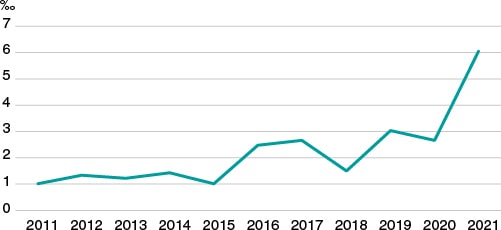
Due to all of this, although it is very possible that doctors can use Bayes’ theorem naturally for his decision-making process regarding diagnosis, prognosis, and treatment, this does not seem to have translated into a significantly wider use of this methodology in research. In an exercise of indirect approach to corroborate the this, we used PubMed to analyze «clinical trial» or «randomized clinical trial» publications in the cardiovascular field over the last 10 years. Then, we selected those where the term «Bayesian» was included somewhere in the text field. Like figure 1 shows—although it has increased significantly over the last few years—the overall rate of possible use of Bayesian methodology in clinical trials in the cardiovascular field is well under 7‰.

Figure 1. Clinical trials published over the last 10 years in the cardiovascular field with possible Bayesian methodology (for every 1000 cardiovascular publications).

If, like Armero et al.1 say, the Bayesian protocol is easy-to-use, robust, and conceptually powerful, why is it used so marginally compared to frequentist statistics? We believe there are several reasons for this. In the first place, frequentist statistics was the first ever used to answer research questions in medicine possibly because right from the start the most common probability distributions had already been perfectly defined, and it was easy to apply the inferential method for decision-making based on such distributions with perfectly defined parameters. However, analytical and computer problems associated with the use of Bayes’ theorem to estimate probabilities were not initially resolved. Secondly, because of the simplicity of being able to make decisions on whether a treatment, diagnostic method, procedure, etc. is effective or not based on the selection of P value < .05 so popular in the frequentist method also referred to by Armero et al. Finally, because the Bayesian conception of probability allocation to parameters and being able to establish direct probabilistic assessments means that the parameter is not an immovable fixed reference anymore. From the analytical standpoint this is a change of paradigm we are not used to. But maybe this loss also generates certain anxiety: parameters are not unchangeable anymore.

FUNDING

None reported.

CONFLICTS OF INTEREST

The authors did not declare any conflicts of interest in relation to this manuscript.

REFERENCES