Durante su primera guardia, un residente de segundo año de cardiología recibe un mensaje de busca por un paciente que acude a urgencias con dolor torácico. En concreto, se le solicita descartar que el dolor sea de origen coronario. El residente interroga al paciente por la sintomatología, examina los factores de riesgo y analiza el electrocardiograma (ECG). Con los datos de este, la información cualitativa del dolor que le relata el paciente y la información de la historia clínica, finalmente descarta que el dolor sea coronario. En la historia clínica registra lo siguiente: «la sintomatología descrita por el paciente, la presencia de hipertensión como único factor de riesgo y la ausencia de cambios específicos del ECG sugieren muy baja probabilidad de dolor de origen coronario». De forma intuitiva, el residente considera que la probabilidad de que dolor sea causado por una enfermedad coronaria (EC), con los datos disponibles (datos cualitativos del dolor, factores de riesgo, ECG), es menor, por ejemplo, del 5%. Dicho de otra manera, el residente instintivamente concluye que:
p(EC|datos cualitativos, factores de riesgo, ECG) < 0,05,
es decir, que la probabilidad de padecer EC condicionada a toda la información anteriormente descrita (datos cualitativos, factores de riesgo y ECG) es menor del 5%.
Sin embargo, antes de dar el alta al paciente decide consultar al residente de quinto año de cardiología que se encuentra en la Unidad de Críticos Cardiológicos. Este acude a urgencias para interrogar de nuevo al paciente por la sintomatología, examinar la historia clínica y analizar el ECG. El residente de quinto año, con mucha más experiencia, considera que, aunque efectivamente no hay factores de riesgo aparte de la hipertensión, ciertas características del dolor podrían ser compatibles con un origen coronario. No solo eso, el análisis del ECG revela mínimas alteraciones de la repolarización, en forma de una muy ligera rectificación del ST, casi imperceptible. De forma intuitiva, el residente considera que la probabilidad de que el dolor sea causado por una EC es sin duda mayor del 5%, y muy posiblemente mayor del 20%. Dicho de otra manera, el residente de quinto año intuitivamente concluye que:
p(EC|datos cualitativos, factores de riesgo, ECG) > 0,2
es decir, que la probabilidad de padecer EC condicionada a toda la información anteriormente descrita (datos cualitativos, factores de riesgo y ECG) es mayor del 20%.
Con esta valoración inicial, el residente de quinto año decide realizar un ecocardiograma transtorácico (ETT), que revela alteraciones de la contractilidad segmentaria. Con esta nueva información, el residente considera que se incrementa sustancialmente la probabilidad de que el origen del dolor sea coronario:
p(EC|datos cualitativos, factores de riesgo, ECG, ETT) > 0,5
La intuición de una probabilidad moderada-alta de origen coronario del dolor al añadir la información del ETT sugiere realizar un análisis de troponina (Tp) de alta sensibilidad, que aparece mínimamente elevada, por lo que la probabilidad intuitiva de un problema coronario como causa del dolor aumenta de manera muy significativa:
p(EC|datos cualitativos, factores de riesgo, ECG, ETT, Tp) > 0,8
El ejemplo previo, a pesar de ser un tanto simplista, ilustra varios hechos en relación con la probabilidad condicionada y, más concretamente, con el clásico teorema de Bayes.
En primer lugar, muestra cómo el teorema de Bayes es una aproximación matemática posiblemente muy apropiada para modelizar nuestra forma natural e intuitiva de tomar decisiones en medicina: a partir de un efecto, que es lo que nos encontramos en la cabecera del paciente (dolor torácico), tomamos una decisión sobre la causa del efecto, con fines diagnósticos, pronósticos o de tratamiento, y asignamos intuitivamente una probabilidad a la causa que consideramos (enfermedad coronaria). Esto lo hacemos a partir de la información disponible que consideramos efectos de la causa y otras variables estrechamente asociadas a la causa: características del dolor, hallazgos del ECG, factores de riesgo, etc.
En segundo lugar, muestra cómo diferentes fuentes de información añadidas de manera secuencial van definiendo de un modo cada vez más preciso la probabilidad de una causa determinada, siempre intuitivamente. No solo eso, en la actividad clínica habitual, la in-
terpretación de las diferentes fuentes de información puede variar de un observador a otro, lo que determinará que la probabilidad asignada a una causa determinada varíe de forma significativa entre varios observadores, en lo que indudablemente desempeña un papel esencial la experiencia del clínico.
El ejemplo también ilustra de manera indirecta la dificultad para obtener estimaciones numéricas, aunque sean aproximadas, de la probabilidad real de la causa (EC) a partir de los efectos observados y de otras variables asociadas a la causa. Como describen Armero et al.1 en un artículo recientemente publicado en REC: Interventional Cardiology, la estimación precisa de la probabilidad del ejemplo exigiría resolver la ecuación del teorema de Bayes:
p(EC|información disponible) = 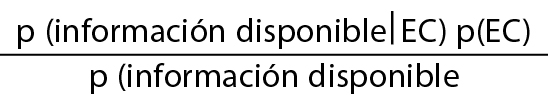
siendo la información disponible, en el ejemplo, los datos cualitativos del dolor, los factores de riesgo, el ECG, etc. Y aquí surgen los problemas. El primero de ellos, como bien ilustran Armero et al.1, es la obtención de la distribución previa para estimar probabilidades. Si bien se pueden hacer estimaciones de la probabilidad de EC en una población a partir de su prevalencia, o podemos estimar la probabilidad de hipertensos o incluso de tener un ECG anormal, la estimación de la probabilidad de los datos cualitativos del dolor no tiene una distribución clara en la que apoyarse. El segundo de los problemas, como también señalan Armero et al.1, es la implementación de una expresión analítica para la distribución a posteriori de los parámetros y para estimar la función de verosimilitud. De nuevo, si bien puede ser factible conocer la probabilidad de ser hipertenso teniendo EC, o de tener un ECG con unas características determinadas teniendo EC, el problema se complica cuando combinamos diferentes fuentes de información: ¿cuál es la probabilidad de tener dolor torácico de ciertas características en un paciente hipertenso, con un ECG determinado, sabiendo que tiene EC? Aunque es verdad que se pueden simular muestras de las distribuciones, además de complicarse el método analítico, como comentan Armero et al.1, posiblemente la interpretación deje de ser intuitiva.
A lo anterior, también habría que añadir el potencial problema del «conocimiento experto» para definir una distribución previa. Como se ha querido mostrar con el ejemplo, el conocimiento puede ser dependiente de la interpretación del experto. Pero es que, además, el conocimiento previo puede estar afectado en gran medida por el sesgo de publicación, o puede simplemente ser erróneo, por lo que la distribución informativa asociada dará lugar a estimaciones de probabilidad sesgadas.
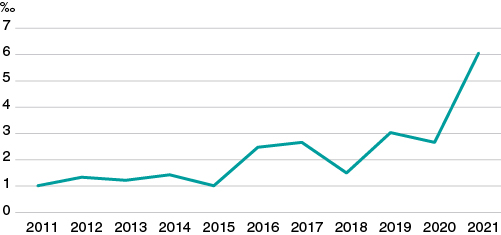
Quizá por todo esto, aunque es muy posible que el médico utilice de manera natural el teorema de Bayes en las decisiones que toma en cuanto a diagnóstico, pronóstico y tratamiento, ello no parece haberse traducido en un incremento importante del uso de esta metodología en la investigación. En un ejercicio de aproximación indirecta para corroborar lo anterior, analizamos en PubMed las publicaciones de tipo «clinical trial» o «randomized clinical trial» del área cardiovascular en los últimos 10 años, y de ellas seleccionamos las que incluyen el término «bayesian» en algún campo del texto. Como se puede ver en la figura 1, aunque hay un incremento significativo en los últimos años, la tasa global de posible uso de metodología bayesiana en ensayos clínicos del área cardiovascular está consistentemente por debajo del 7‰.
Figura 1. Ensayos clínicos publicados en los últimos 10 años en el área cardiovascular con posible metodología Bayesiana (por cada 1000 publicaciones cardiovasculares).
¿Por qué entonces, si el protocolo bayesiano, como afirman Armero et al.1, es sencillo y robusto y conceptualmente potente, se usa de un modo tan marginal en comparación con la estadística frecuentista? Pensamos que hay varias razones. En primer lugar, la estadística frecuentista fue la primera que se utilizó para contestar preguntas de investigación en medicina, posiblemente porque desde un buen inicio estaban muy bien definidas las distribuciones de probabilidad más habituales y era sencillo aplicar el método inferencial para tomar decisiones basadas en dichas distribuciones con parámetros perfectamente definidos. Por el contrario, los problemas analíticos y computacionales asociados al uso del teorema de Bayes para estimar probabilidades no estaban inicialmente resueltos. En segundo lugar, por la simplicidad de poder tomar una decisión sobre si un tratamiento, un método diagnóstico, un procedimiento, etc., es eficaz o no lo es mediante la selección de un valor de p < 0,05, tan popular en el método frecuentista y al que también hacen referencia Armero et al.1 en su artículo. Y por último, porque la concepción bayesiana de asignar probabilidades a parámetros y poder establecer valoraciones probabilísticas directas supone que el parámetro deja de ser un referente fijo e inamovible. Esto, sin duda, constituye un cambio conceptual desde el punto de vista analítico al que no estamos habituados. Pero, además, quizá genere cierta ansiedad esa pérdida: los parámetros han dejado de ser inmutables.
FINANCIACIÓN
Ninguna.
CONFLICTO DE INTERESES
Los autores declaran no tener conflictos de intereses en relación con el presente documento.